I really enjoy folding origami, and I think it’s really cool how you can make such nuanced objects out of something as plain as a square sheet of paper. Below is one of my favorite models, the Fiery Dragon by Kade Chan.

To more deeply explore the art of origami, I pursued an independent study this past fall semester titled “Mathematics of Origami.” Here are some of the most interesting things I learned:

Dividing a paper into an n × n grid:
Have you ever wanted to divide a square into an n × n grid but didn’t have a ruler on hand? Fear not! There exists a simple way to create such a grid for any integer n using nothing more than folding. If n is a power of two, we’re good: fold the paper in half, then fold each half into halves to get quarters, then halve each quarter to get eighths, and so on and so forth. If n is not a power of two, we can use the magic of similar triangles to construct a regular n × n grid. Here’s an example for the 3 × 3 case:
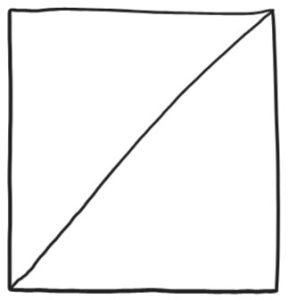
1. Make a diagonal crease from the bottom left corner to the top right corner.

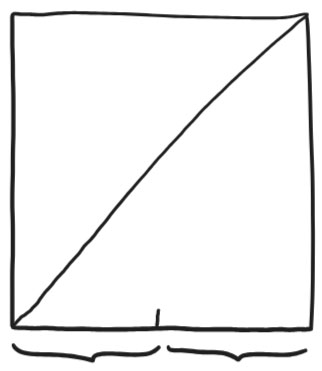
2. Mark the midpoint of the bottom edge by folding the left edge to the right edge.

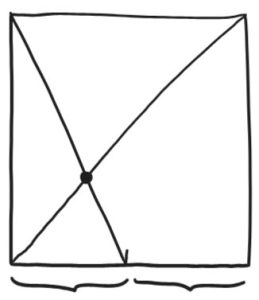
3. Make a crease from the top left corner to the midpoint of the bottom edge. The point where this crease intersects the diagonal one we first made is located a third of the way from the left to the right edge, and a third of the way from the bottom to the top one.

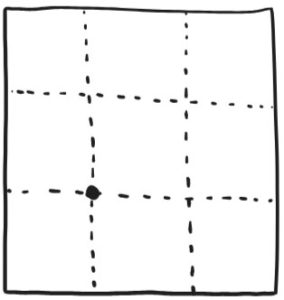
4. Complete the grid by making vertical and horizontal creases at the point, then folding the top and right edges to the point.

Tree theory:
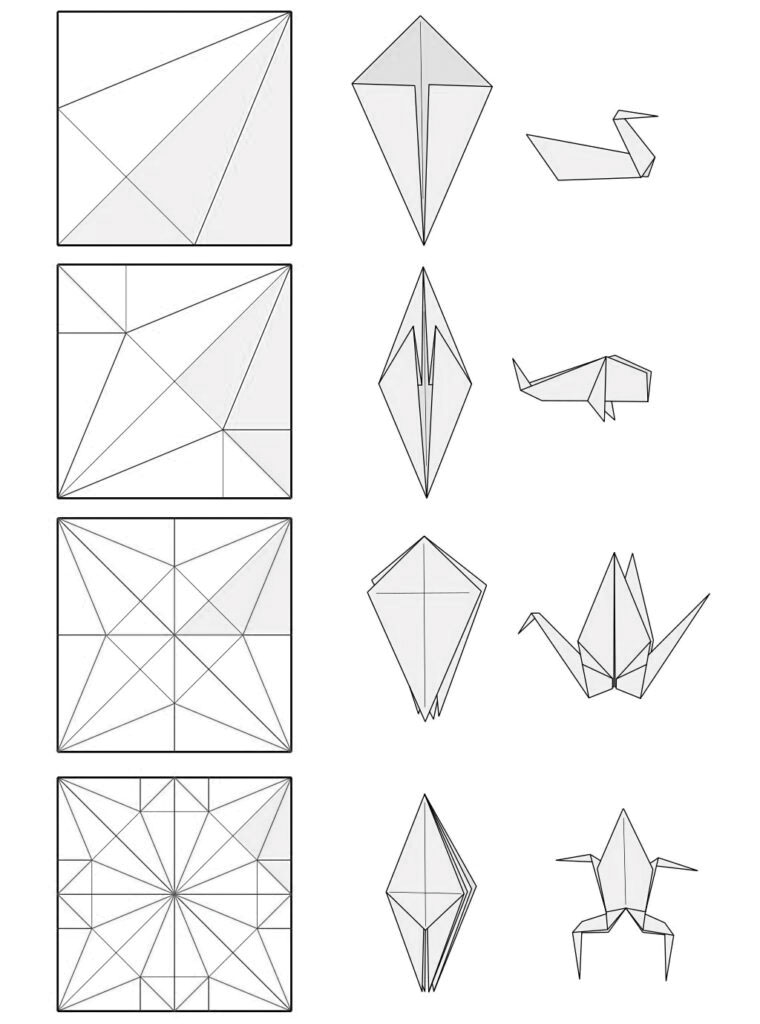The foundation of most traditional origami models are these three bases: fish, crane, and frog. In the mid to late 1900s, a couple master origamists (such as Toshiyuki Meguro and Robert Lang) devised structures called uniaxial bases to make more complex shapes. These allow one to fold any tree, mathematically guaranteed (don’t worry if you don’t know exactly what those terms mean).

For instance, let’s say we wanted to make some lizard with a head, two front legs, a long body, two hind legs, and a tail. Here’s the corresponding tree, i.e., a simple outline of the shape we want:

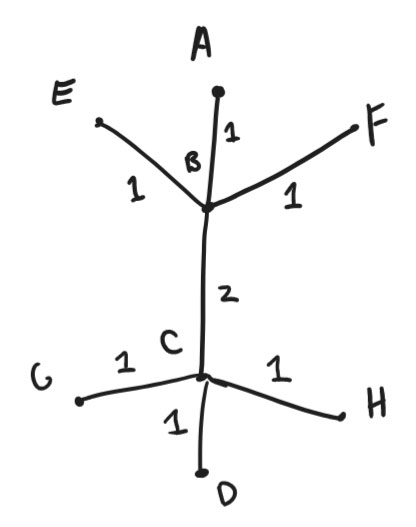
We can specify points, edges that link them, and the lengths of each edge. There exists an algorithm to turn this tree into a crease pattern that folds into a 3D version of the tree, which is called a uniaxial base.

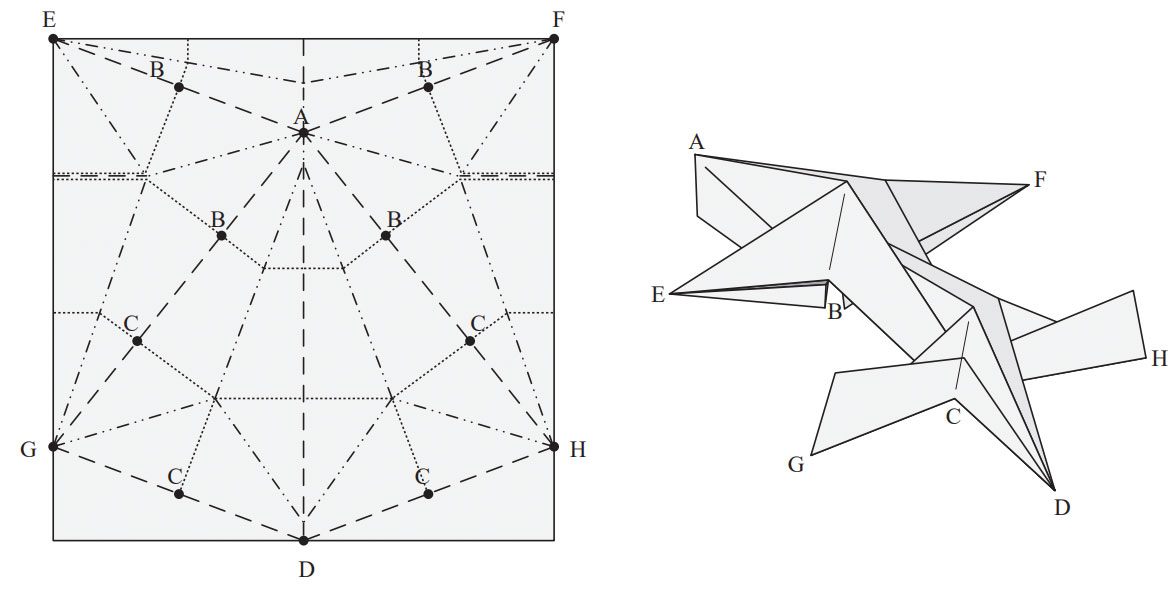
Robert Lang wrote a piece of software to perform this algorithm for us, and it’s called TreeMaker.

Margulis napkin problem:
This problem, named after Russian-American mathematician Grigory Margullis and posed by Soviet-Russian mathematician Vladimir Arnold in 1956, concerns whether it’s possible to fold a square into a polygon with greater perimeter than it started with. With tree theory, this can be done! No cutting or stretching the paper is required. Here’s the crease pattern of one such solution:

If you pack an n × n square grid of spikes into the paper and each has a radius of 1/n, the total length of all the spikes will be n × n × 1/n = n. Therefore, if we let n grow large and create a ridiculous number of very small circles, it’s possible (in theory) to achieve arbitrarily high perimeters with this method. But that’s maybe just a little impractical.

Box pleating:
Most complex models these days are made with a variation of the tree method called box pleating. One starts with a tree, then maps it onto a square grid. This method is slightly more extensible than the standard tree-making method, though requires the paper to be pre-creased into a grid beforehand. People have made really crazy stuff with this! Here’s the diagram for Jo Nakashima’s praying mantis, which takes place on a 48 × 48 grid:

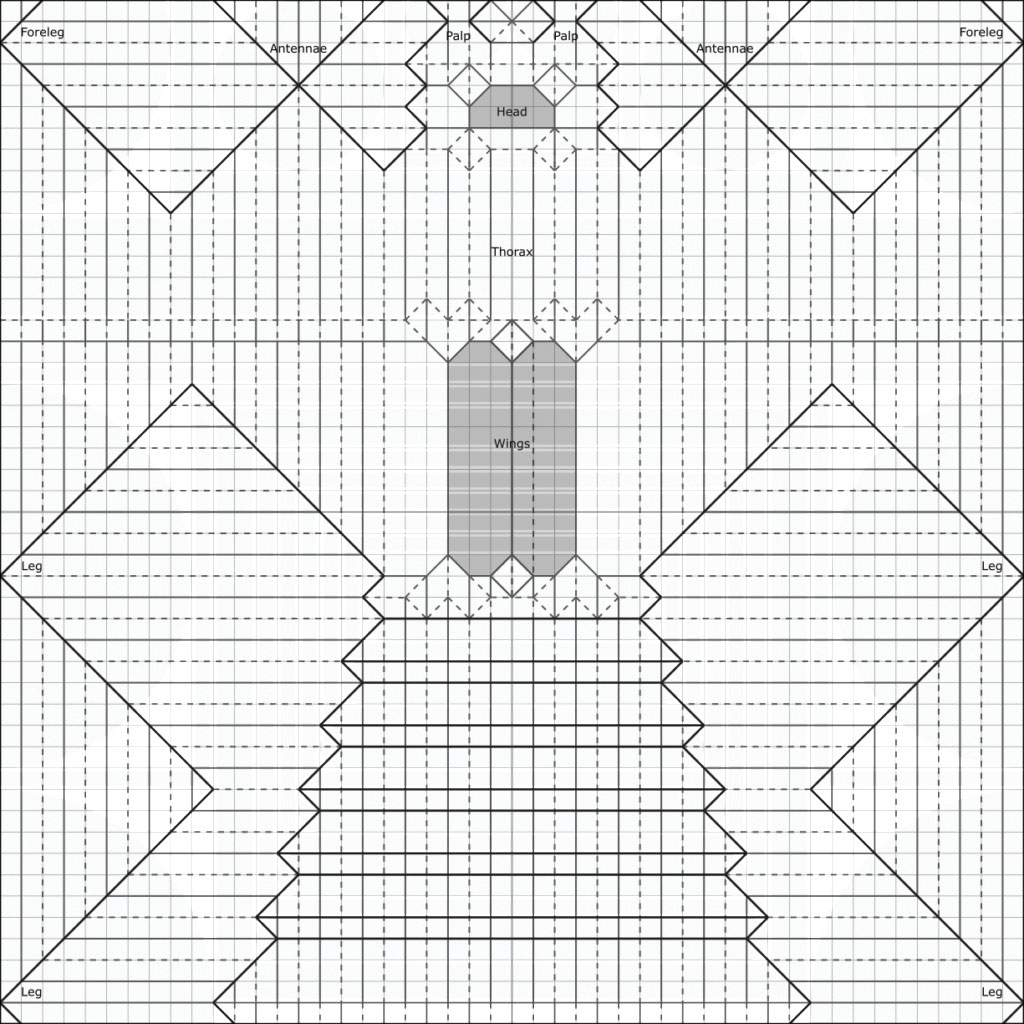
Every node in the tree is represented by a circle, and eventually becomes a limb or flap on the final model. I folded the praying for my independent study final project:

I’ll leave with a much more complex box-pleated model from origami designer and artist Boice Wong:

Conclusion:
At various points in my study, I encountered some tension between mathematical theory and practical application. For instance, it’s possible to fold any polygon imaginable from just a single square sheet by first pleating it down to a narrow strip and then “twisting” it around. Is that practical? Absolutely not. The paper would get way too thick and way too small. But it’s nice to know that, at least in theory, it’s possible to make anything. On the other end, there are very practical theoretical results, such as tree theory and box pleating. From these techniques, people have derived the most complex models known to date.

Although origami has existed for thousands of years, the use of mathematics and computation in the art has developed only very recently (about mid-20th century). It’s really cool to see these modern tools being applied to such an ancient art, and I can only imagine what kinds of ever-more-amazing things will come up through this fusion in the future.